Quick Navigation
- What is the Future Value Formula, Really?
- Putting the FV Formula to Work: Real Scenarios
- The Devil's in the Details: Key Factors That Change Everything
- Future Value vs. Present Value: Two Sides of the Same Coin
- Common Questions (And My Frank Answers)
- Limitations and Why You Shouldn't Worship the Formula
- Getting Practical: Your Action Plan
Let's be honest. When most people hear "future value formula," their eyes glaze over. It sounds like something reserved for Wall Street quants or your accountant during tax season. I used to think the same way. I remember staring at a retirement calculator, punching in numbers, and having zero clue how it spat out that final figure. It felt like magic, and not the good kind. It felt like I was just hoping for the best.
That's a terrible way to plan your financial future.
Then I actually learned the future value formula. Not just memorized it, but understood what each piece meant. And let me tell you, it was a game-changer. It didn't make me a stock-picking genius, but it did something more important: it took the guesswork out of my goals. Want to know if you're saving enough for a house down payment in 5 years? Curious how that $5,000 investment might grow by the time you retire? The future value formula (or FV formula, as it's often called) gives you a flashlight in the dark tunnel of long-term planning.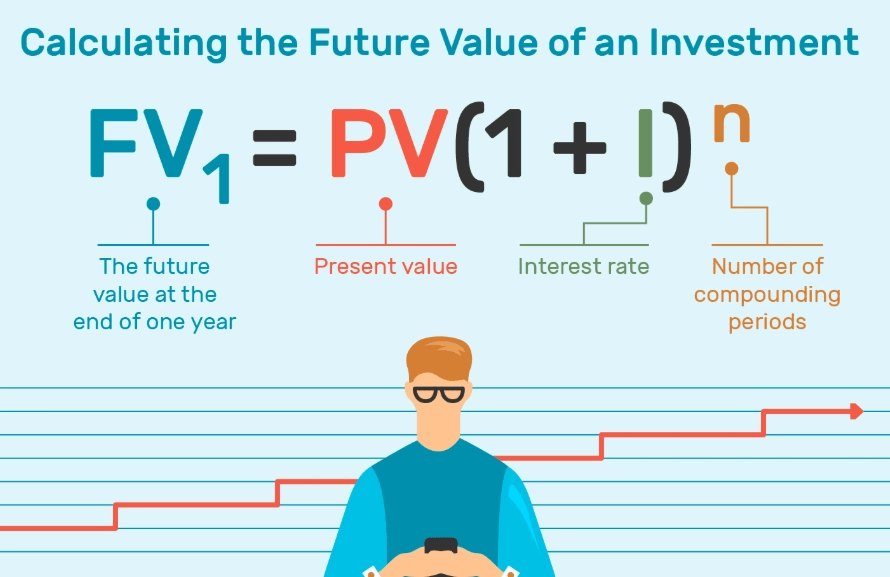
This guide is that flashlight for you. We're going to break this thing down into plain English, step away from the textbook theory, and focus on what you actually need to know to make smarter decisions with your money.
What is the Future Value Formula, Really?
At its heart, the future value formula is a way to answer one simple question: What will my money be worth later?
It's the mathematical core of the idea that money today is worth more than the same amount tomorrow. That's the time value of money. A dollar in your hand now can be invested and earn a return. A dollar promised to you in the future can't. The FV formula quantifies that difference.
Looks simple, right? It is. But each of those letters holds the key. Let's unpack them without the jargon.
- FV (Future Value): This is the answer you're looking for. The total amount your money will grow to in the future.
- PV (Present Value): This is your starting line. It's the lump sum of money you have right now that you're going to invest or save. Think: an initial deposit, a bonus from work, an inheritance.
- r (Rate of Return per Period): This is the engine. It's the interest or growth rate you expect your money to earn for each compounding period. This is crucial—if your investment compounds annually, 'r' is the annual rate. If it compounds monthly, you need the monthly rate. This is where many online calculators and people mess up.
- n (Number of Periods): This is the timeline. It's how many compounding periods your money will be growing. Again, this must match your 'r'. 5 years of annual compounding means n=5. 5 years of monthly compounding means n=60 (5 years * 12 months).
The little caret symbol (^) means "to the power of." That exponent is the magic of compounding. It's not just interest on your initial money; it's interest on your interest. Einstein allegedly called it the eighth wonder of the world. He wasn't wrong.
Putting the FV Formula to Work: Real Scenarios
Okay, theory is fine. But how does this play out in your actual life? Let's walk through some concrete examples.
Scenario 1: The Lazy Lump Sum
You get a $10,000 tax refund (lucky you!). Instead of blowing it on a fancy vacation (tempting, I know), you decide to invest it in a broad-market index fund. You're optimistic and hope for an average annual return of 7%. You plan to leave it completely alone for 20 years.
Using the future value formula:
PV = $10,000
r = 7% (or 0.07)
n = 20 years
FV = $10,000 x (1.07)^20
FV = $10,000 x 3.8697
FV = $38,697
That single $10,000 investment could grow to nearly $39,000 in two decades. Not bad for just leaving money alone. But here's the kicker—most of that growth happens in the later years. The first 10 years might get you to around $20,000, but the second 10 years nearly double it again. That's the power of the exponent in the FV formula at work.
Scenario 2: Regular Contributions – The Future Value of an Annuity
The lump sum example is great, but most of us build wealth by saving regularly. This introduces a slightly more complex but far more useful version: the future value of an annuity formula. It calculates the future value of a series of equal payments.
Where Pmt is your regular payment.
Let's say you commit to investing $300 every single month into your retirement account. You expect a 6% annual return, and you'll do this for 30 years. Because you're contributing monthly, we need to adjust the rate and periods.
- Monthly payment (Pmt) = $300
- Annual rate = 6%, so Monthly rate (r) = 6%/12 = 0.5% (or 0.005)
- Number of periods (n) = 30 years * 12 months = 360
FV = $300 x [ ((1 + 0.005)^360 - 1) / 0.005 ]
FV = $300 x [ ((1.005)^360 - 1) / 0.005 ]
FV = $300 x [ (6.0226 - 1) / 0.005 ]
FV = $300 x [ 5.0226 / 0.005 ]
FV = $300 x 1004.52
FV = $301,356
Let that sink in. By consistently investing $300 a month—that's about $10 a day—you could potentially amass over $300,000. The total you contributed was only $108,000 ($300 x 360 months). The rest, nearly $200,000, is pure growth generated by the future value formula's compounding engine. This is why starting early is the single biggest advantage you have.
The Devil's in the Details: Key Factors That Change Everything
If you just use the basic FV formula with optimistic numbers, you'll get an optimistic result. But the real world is messier. To use this tool effectively, you have to wrestle with a few critical details.
Compounding Frequency: The Silent Multiplier
How often your interest is calculated and added to your principal makes a massive difference. Annual compounding is simple, but many accounts compound monthly, quarterly, or even daily. The more frequent the compounding, the higher the final future value.
Look at this comparison for a $10,000 investment at a 5% annual interest rate over 10 years.
| Compounding Frequency | Future Value | Notes |
|---|---|---|
| Annually | $16,288.95 | Standard calculation, simplest. |
| Semi-Annually | $16,386.16 | Rate becomes 2.5% (5%/2), periods become 20. |
| Quarterly | $16,436.19 | Rate becomes 1.25% (5%/4), periods become 40. |
| Monthly | $16,470.09 | Rate becomes ~0.4167% (5%/12), periods become 120. |
| Daily | $16,486.65 | Rate becomes ~0.0137% (5%/365), periods become 3650. |
See? The difference between annual and daily compounding on this example is almost $200. Over longer timelines and larger sums, this gap widens significantly. Always check how your investment compounds!
The Rate of Return (r): The Grand Illusion
This is the trickiest part. Picking a realistic 'r' is more art than science. Plugging in 10% because you heard that's the stock market average is a classic mistake. That's a historical average before inflation, costs, and taxes. Your real-world return will be lower.
For a more authoritative take on realistic expectations for compound growth, the U.S. Securities and Exchange Commission (SEC) provides clear explanations and tools. Their Compound Interest Calculator and related materials are a fantastic, unbiased resource to ground your assumptions.
Taxes and Fees: The Growth Killers
The standard FV formula assumes your growth is tax-free and fee-free. That's almost never true. Investment fees (expense ratios, advisory fees) directly eat into your 'r'. Taxes, depending on the account type (taxable vs. IRA/401k), can take a big bite out of your returns when you sell or receive dividends.
My personal rule of thumb? When doing a quick future value calculation, I shave at least 1-1.5% off the expected return rate to account for fees and tax drag. It's a blunt instrument, but it prevents me from getting too carried away with the numbers.
Future Value vs. Present Value: Two Sides of the Same Coin
Often, you'll see the future value formula's sibling: the present value formula. It answers the reverse question: What is a future sum of money worth to me right now?
This is incredibly useful for evaluating opportunities or debts.
Imagine you're offered $20,000 five years from now. What's that worth today? If you could otherwise invest money at a 4% return, you'd calculate:
PV = $20,000 / (1 + 0.04)^5
PV = $20,000 / 1.21665
PV = $16,438.85
That $20,000 in five years is only "worth" about $16,439 to you today, given your 4% alternative.
This is why winning a lottery that pays out $1 million over 20 years isn't the same as getting $1 million today. The present value of that annuity is much lower. Banks use this principle all the time when structuring loans and payments.
Common Questions (And My Frank Answers)
Here are the questions I had, and the ones I see pop up all the time.
Is the future value formula accurate for stock market investing?
No, and anyone who tells you it is, is oversimplifying. The FV formula assumes a steady, constant rate of return ('r'). The stock market is volatile—it goes up and down. The formula gives you a projection or an estimate based on an average. It's a planning tool, not a prophecy. Use it to set savings targets and understand the power of compounding, not to predict your exact account balance on a specific date.
How do I account for inflation in my FV calculations?
You have two good options, and I prefer the second one.
- Use a "real" rate of return: Subtract your expected long-term inflation rate from your expected investment return. Expected Return (8%) - Expected Inflation (3%) = Real Rate (5%). Use 5% as 'r' in your formula. Your result will be in "today's dollars," which is much easier to conceptualize.
- Calculate in nominal terms, then deflate: Do the FV calculation with your full expected return (e.g., 8%). This gives you a future number in "future dollars." Then, use an inflation calculator to see what that amount might feel like in today's purchasing power. The U.S. Bureau of Labor Statistics has a reliable CPI Inflation Calculator for this exact purpose.
Can I use the FV formula for debt (like credit cards)?
Absolutely, and it's terrifyingly enlightening. The future value formula shows how debt snowballs. If you have a $5,000 credit card balance at 18% APR (that's 1.5% monthly) and you make no payments, the formula shows how much you'll owe.
FV = $5,000 x (1 + 0.015)^12 (for one year)
FV = $5,000 x (1.1956)
FV = $5,978
In one year of doing nothing, you'd owe nearly $6,000. This is why minimum payments often feel like running on a treadmill—you're barely covering the new interest, so the principal (your PV) never goes down. Run this calculation next time you're tempted to carry a balance.
Limitations and Why You Shouldn't Worship the Formula
I love this tool, but I don't trust it blindly. It has blind spots.
First, it's purely mathematical. It doesn't factor in life. A job loss, a medical emergency, a change in goals—these can derail the cleanest future value calculation. Your plan needs flexibility, not just a number at the end of a spreadsheet.
Second, it can create an illusion of precision. Getting a result like $1,243,567 for your retirement can make you feel like you've "solved" it. You haven't. You've just modeled one possible path based on your best-guess inputs. The real value isn't the final number; it's the understanding of the relationship between your savings rate, your time horizon, and your expected return.
Finally, focusing solely on maximizing future value can lead to bad present decisions. Hoarding every penny for a future number might mean missing out on meaningful experiences today. Balance is key. The formula is a guide for your financial journey, not the dictator of your life's choices.
Getting Practical: Your Action Plan
Don't just read this. Do something with it.
- Play with a calculator. Use the SEC's calculator I linked earlier. Put in your own numbers. See what happens if you start saving $50 more a month. See the dramatic impact of starting 5 years earlier.
- Run a "retirement sanity check." Take your current retirement savings as PV. Use a conservative real return (like 4-5%). Use the number of years until you retire as 'n'. What's the FV? How does it compare to what you think you'll need? The gap might motivate you.
- Use it for your next goal. Want a $30,000 down payment in 3 years? Work backwards. If you can earn 2% in a savings account, how much do you need to save as a lump sum today (PV)? Or how much monthly (using the annuity formula)?
The future value formula isn't just for finance nerds. It's a fundamental lens for viewing any decision involving time and money. It empowers you to move from hoping to knowing, from guessing to planning. It won't guarantee success, but it will dramatically increase your odds of getting where you want to go. And that, in my opinion, is worth its weight in gold—both present and future.