Quick Guide to This Article
- How to Actually Find the Mode (Step-by-Step, Without the Headache)
- When the Mode Gets Tricky: Bimodal, Multimodal, and No Mode at All
- Mode vs. Mean vs. Median: The “Average” Family Feud
- Real-World Uses of the Mode (It's More Useful Than You Think)
- Common Pitfalls and How to Avoid Them
- Your Mode Definition Math Questions, Answered
- Wrapping It Up: The Mode as a Storyteller
Let's be honest, when you first heard about the "mode" in math class, you probably thought it was the easiest thing ever. Just find the number that shows up the most, right? Well, sort of. But then things got weird. What if there's a tie? What if no number repeats? Suddenly, that simple mode definition math concept starts to feel a bit slippery.
I remember trying to explain it to a student once. We had a dataset of shoe sizes, and there were two numbers that appeared twice. He looked at me and said, "So... which one is it?" That's the moment I realized the textbook definition often leaves out the messy, interesting parts. The real-world parts.
So, let's ditch the robotic textbook language. We're going to talk about the mode like two people figuring something out over coffee. What is it really? When do you actually use it? And why does it sometimes feel less useful than its siblings, the mean and median?
At its absolute core, the mode is the value that appears most frequently in a given set of data. It's the champion of popularity in a number lineup. If data were a party, the mode would be the snack everyone keeps going back for.
You'll see the mode definition math experts use is just that. But that simplicity is deceptive. The devil, as they say, is in the details—or in this case, in the duplicates.
How to Actually Find the Mode (Step-by-Step, Without the Headache)
Forget the complicated algorithms for a second. Finding the mode is a process of organized counting. Here’s how a human brain does it, not a computer.
First, you list your data. I don't care if it's in order yet, just get it out of your head and onto paper or a screen. Let's use a real, slightly messy example. Say you surveyed 15 friends about how many cups of coffee they drank yesterday. Your data looks like this:
1, 3, 2, 4, 0, 2, 3, 2, 5, 1, 2, 3, 2, 1, 4
Now, start tallying. How many people said "0"? Just one. How many said "1"? Let's count... one, two, three. Three people. "2"? One, two, three, four, five. Five people. Keep going. "3" appears three times. "4" appears twice. "5" appears once.
Look at your tallies. The number "2" has the highest tally (five). So, the mode is 2. That's it. The most common number of coffee cups in your friend group was two. The mode definition math problem is solved.
When the Mode Gets Tricky: Bimodal, Multimodal, and No Mode at All
This is where most explanations stop, and where the real confusion begins. What happens when your data doesn't play nice?
Let's use a table to make sense of these different scenarios. It's much clearer than a wall of text.
| Scenario | What It Means | Example Dataset | The Mode(s) | Real-World Analogy |
|---|---|---|---|---|
| Unimodal | One clear winner. A single value appears most often. | Shirt Sizes: S, M, M, L, M, S, M | M | A song that's clearly the most played on your playlist. |
| Bimodal | Two-way tie for first place. Two distinct values are equally frequent. | Test Scores: 70, 85, 90, 85, 70, 90, 80 | 70 & 90 | A store finds two equally popular colors for a t-shirt. |
| Multimodal | Three or more values are tied for the top frequency. | Pet Types: Dog, Cat, Cat, Bird, Dog, Bird, Fish | Cat, Dog, Bird | A poll where three political candidates are virtually tied. |
| No Mode | Every value is unique. There are no repeats. | Roll of a Die: 1, 2, 3, 4, 5, 6 | No mode exists. | Every person in a room has a different birthday. |
Bimodal data is fascinating. It often hints at two different groups within your dataset. Those test scores? Maybe they suggest one group of students who studied one way and another group who studied differently. Recognizing this is a superpower the simple mode definition math gives you.
And “no mode” isn't a failure. It's valuable information! It tells you your data is highly varied, with no central tendency toward a single repeated value. Reporting "no mode" is a perfectly valid answer.
Mode vs. Mean vs. Median: The “Average” Family Feud
This is the big one. Why do we have three different “averages”? They each tell a different story, and picking the wrong one can give you a totally misleading picture.
Let me tell you about a small business owner I know. She was looking at her employees' salaries to get a sense of a “typical” pay. The mean (the arithmetic average) was quite high because the two owners paid themselves large salaries. The median (the middle value) was lower and more representative of the regular staff. But the mode? That was the entry-level salary, which was the most common single pay point in the company.
Each number was “correct,” but each answered a different question.
The Mean answers: "If we redistributed everything equally, what would everyone get?" It's sensitive to extreme values (outliers). One billionaire in a town skyrockets the mean income.
The Median answers: "What’s the middle-of-the-road value?" It splits the data set in half. It's robust against outliers. The billionaire doesn't affect it much.
The Mode answers: "What is the most common or popular value?" It identifies clusters and high-frequency outcomes. It's the only one you can use for categorical data (like “favorite color”).
So, when should you use the mode specifically? Use it when the "most frequent" occurrence is what matters most. Think about a shoe store deciding what sizes to stock the most of. They don't care about the “average” foot size (mean) or the “middle” foot size (median). They desperately need to know the most common foot sizes (the modes) to avoid stocking shelves with sizes nobody buys. This practical application is the heart of the mode definition math in action.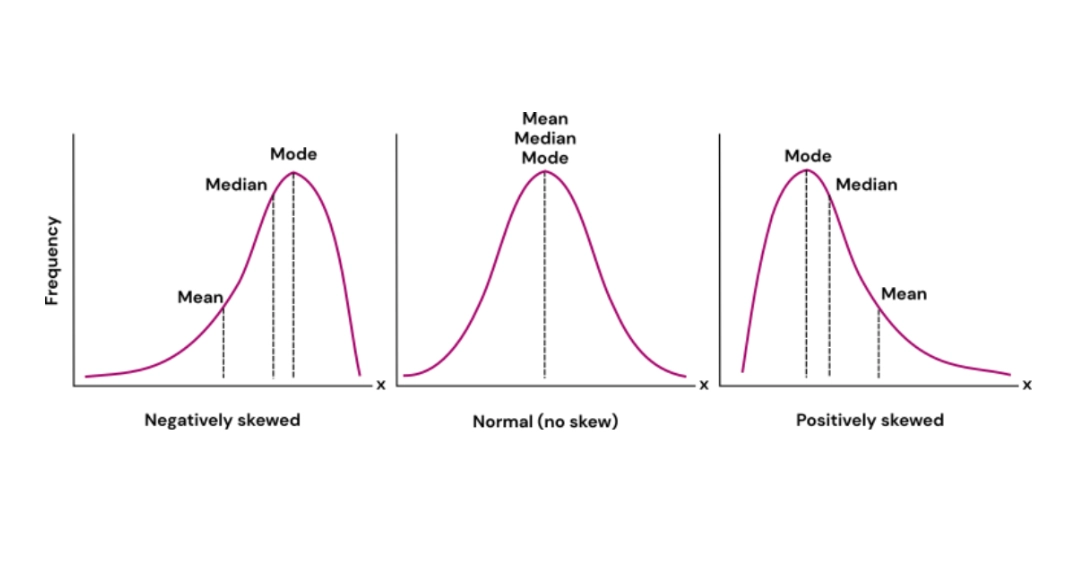
Real-World Uses of the Mode (It's More Useful Than You Think)
People sometimes dismiss the mode as the least useful measure of central tendency. I think that's because they only see the silly textbook examples. In the real world, the mode is a secret weapon for decision-making.
- Retail & Inventory: We touched on this. The most common size, color, or product model dictates stock orders. This is pure, applied mode definition math.
- Customer Feedback: If 100 people complain about 20 different things, but 40 of them complain about “slow shipping,” the mode of the complaint categories clearly points to the top priority.
- Public Policy: What's the most common household size? The most frequent reason for emergency room visits? These modal values help governments plan housing, allocate resources, and design public health campaigns. The U.S. Census Bureau uses these concepts constantly to understand American life.
- User Experience (UX) Design: Designers track the most common path users take through an app or website (the modal path). If 70% of users click “A” then “B,” that flow should be optimized and made bulletproof.
It’s also the only measure you can use for categorical or non-numerical data. You can't calculate the mean or median of “dog, cat, bird, dog.” But you can easily see the mode is “dog.”
Common Pitfalls and How to Avoid Them
I've graded enough papers to know where students trip up. Here are the big mistakes, straight from the “I've seen it” files.
- Forgetting to Count All Occurrences: In a rush, it's easy to glance at data and guess. Always, always tally. For the dataset 1, 1, 2, 3, 1, 2, the mode is 1 (appears three times), not 2.
- Misidentifying Bimodal Data: If two numbers tie, you must report both. Don't just pick the first one or the bigger one. The correct answer for 5, 7, 5, 7, 8 is “5 and 7.”
- Confusing “No Mode” with “Mode is Zero”: This is a classic. If your data is 0, 0, 1, 2, the mode is 0 (it repeats). If your data is 1, 2, 3, 4, there is no mode. Zero is a number like any other.
- Ignoring the Data Type: Trying to find a mean or median for categories (like “red, blue, green”) is nonsense. But finding the mode is perfectly valid and useful.
Pro Tip: When writing your answer, be specific. Don't just say “the mode is 2.” Say “The mode is 2, as it appears five times, which is more frequent than any other value.” This shows you understand the mode definition math beyond just the answer.
Your Mode Definition Math Questions, Answered
Here are the questions I get asked all the time, the ones that pop up in search bars after “what is mode in math.”
Wrapping It Up: The Mode as a Storyteller
At the end of the day, the mode isn't just a calculation. It's a way to listen to what your data is trying to tell you about frequency and preference. It points to the biggest cluster, the most popular choice, the repeated pattern.
Is it always the best measure? No. For skewed numerical data, the median often tells a fairer story. For many engineering applications, the mean is essential. But for answering “what happens most often?”—whether it's shoe sizes, website clicks, or survey responses—the simple, humble mode is your go-to tool.
So next time you encounter a mode definition math problem, don't just robotically find the number. Think about what that most frequent value represents in the real world. That's where the true understanding—and utility—lies.